So Again, Party Of Science Put Out No Science To Prove This Gender-Fluid, Crap,, What Do They Got A Flu And Need To Drink A lot Of Fluid,

So let Look At  Fluid, Real Women  Drink  Fluid When "Pregnant" And" Real Mean And Real Women Drink Fluids When We Get Sick Or Are They Talking About Pressure in Fluids?, MAY Be They Mean Fluid Mechanics That Got To Be It , You Know Mechanical Engineering? , Come Think About It, It's Going To Be, The Fluid Mosaic Model , That it, There It Is! , No Wait A Minute, I Got  It,There Talking About, Fluid In Lungs, That Got To Be It! We Found It! Party Time! , Nope Fluid In Lungs Was Not It, Well Were S.J.W Come With Gender-Fluid, Crap, There Just No Science To Prove It!





1. Real Women, The Institute of Medicine recommends that pregnant women drink about 10 8-ounce cups of water or other beverages each day.


Women's needs differ, so don't worry if you find yourself needing a bit more or less. You can tell you're getting enough if your urine looks pale yellow or colorless. You're likely to need more fluid than usual in a warm climate, at high altitude, or if you're exercising.


Plain water is an ideal beverage, but milk, juice, coffee, and tea all contain plenty of water and count toward your fluid intake. Keep in mind, though, that juice and sweetened drinks also provide a lot of extra calories, so you don't want to rely on them too much.


It's best to limit caffeine, too, including caffeinated coffee, teas, and sodas. The American College of Obstetricians and Gynecologists (ACOG) advises pregnant women to get no more than 200 milligrams of caffeine per day.


Don't hesitate to drink water and other fluids because you're afraid of retaining water. Oddly enough, fluid retention can result from not drinking enough, because your body will hang on to more fluid if it senses it's becoming dehydrated.


So if your feet and ankles are swollen, drinking more water can actually help. (If swelling is excessive or comes on suddenly, contact your caregiver, as this can be a sign of preeclampsia.)
Fluids also help prevent common pregnancy problems such as constipation, hemorrhoids, and bladder infections. (Drinking water dilutes your urine, which reduces your risk of infection.)
It's especially important to stay hydrated in the last trimester, when dehydration can cause contractions that can trigger preterm labor.


Ten cups might seem like a lot, especially if you're battling nausea during pregnancy. Try sipping water throughout the day rather than drinking a lot at once. If you don't like the taste of water, try adding a lemon or lime wedge or a little juice for additional flavor.

https://www.babycenter.com/404_how-much-water-should-i-drink-while-im-pregnant_5283.bc

2. Real Mean And Real Women fluids to drink when sick.

Best (and Worst) Drinks When You Have a Cold

When you're sick, you hear it over and over: "Get plenty of fluids.” And it’s true. Your body needs extra hydration when you’re trying to get well.

But what, exactly, should you put in your cup? Some drinks are great for easing symptoms, and others may make them worse. Keep these tips in mind when you’re picking what to sip.

Drinks That Help

• Decaf tea. The heat can soothe sore throats, stuffy noses, chest congestion, and upset stomachs. Plus, a warm cup of tea is comforting when you’re feeling rough. If you choose one with herbs like ginger, your immune system may get a small boost, too. For an extra benefit, try adding a small dollop of honey to your cup: it can calm a cough and help you sleep.
• Water with lemon. Hot or cold, it keeps you hydrated and loosens up stuffiness and congestion. Lemon is also high in vitamin C, which may make a cold slightly shorter if you get it regularly.
• Soup. Clear soups and broths give you calories when you may not have much of an appetite. Some research shows they may help relieve inflammation in the body, which can relieve some of your symptoms. The warmth also helps break up mucus.  
• Ice chips or ice pops. True, these aren’t technically a beverage, but they have the same purpose: keeping you hydrated.

What You Don’t Need

These drinks won’t help you get over your cold or flu, and some could do more harm than good. 

• Sports drinks. They can help if you’re very dehydrated, but they don't really do much to make you feel better. Plus, they have a lot of sugar. Other drinks will help you hydrate without the extra sweet stuff.
• Fruit juices. Juice may seem like a good idea, especially for kids, but like sports drinks, most have loads of added sugar. Citrus-based ones like orange juice can also aggravate sore throats. If it's all your child wants to drink, try adding a splash or two to a cup of water instead of a glassful of juice.
• Coffee. If you’re going to sip a hot drink, might as well get your daily dose of caffeine in it, right? Wrong. Caffeine can make you dehydrated, which isn’t good when you’re trying to get well. The same goes for soda and caffeinated teas.
• Ginger ale. While ginger in its natural form may have some cold and flu benefits, this carbonated, sugary version won't offer much relief. Soft drinks of any kind have very little of the nutrients and electrolytes you need to fight off sickness. Get your ginger in a mug of hot tea instead.  
• Alcohol. It dehydrates you and can make some symptoms worse, like nausea, headaches, and body aches. Booze can also make your body less able to handle infections. So save that hot toddy for when you’re feeling better.
• http://symptoms.webmd.com/cold-flu-map/how-to-stay-hydrated-when-youre-sick

3.How do you find the pressure in a fluid?


What does pressure mean?

If you tried to hammer a bowling pin into the wall, nothing would probably happen except for people deciding to no longer lend you their bowling pins. However, if you hammer with the same force on a nail, the nail would be a lot more likely to penetrate the wall. This shows that sometimes just knowing the magnitude of the force isn't enough, you also have to know how that force is distributed on the surface of impact. For the nail, all the force between the wall and the nail was concentrated into the very small area on the sharp tip of the nail. However, for the bowling pin the area touching the wall was much larger, and therefore the force was much less concentrated.

Person hitting a bowling ball and a nail with a hammer.

To make this concept precise, we use the idea of pressure. Pressure is defined to be the amount of force exerted per area.

${\Large P=\dfrac{F}{A}}$P, equals, start fraction, F, divided by, A, end fraction

So to create a large amount of pressure, you can either exert a large force or exert a force over a small area (or do both). In other words, you might be safe lying on a bed of nails if the total surface area of all the nail tips together is large enough.

[Really?]

Yeah, people do this. Since it's the total area over which the force is distributed that counts, the total surface area of all the nails can reduce the pressure that's created by your weight downward. But there has to be a huge number of nails for this to work.

This definition also means that the units of pressure are newtons per square meter $\dfrac{\text{N$

$}}{\text{m}^2}$start fraction, N, divided by, m, start superscript, 2, end superscript, end fraction which are also called pascals or abbreviated as $\text{Pa}$P, a.

[Who was Pascal?]

Blaise Pascal was a 17th century scientist, mathematician, and philosopher. Not only did he contribute the the understanding of fluid pressure, but he is also noted for "Pascal's wager", "Pascal's triangle", and "Pascal's theorem".

(Janmad CC BY 3.0)

How do you find the pressure in a fluid?

A solid surface can exert pressure, but fluids (i.e. liquids or gases) can also exert pressure. This might seem strange if you think about it because it's hard to imagine hammering in a nail with liquid. To make sense of this, imagine being submerged to some depth in water. The water above you would be pushing down on you because of the force of gravity and would therefore be exerting pressure on you. If you go deeper, there will be more water above you, so the weight and pressure from the water would increase too.

Not only can the weight of liquids exert pressure, the weight of gases can as well. For instance, the weight of the air in our atmosphere is substantial and we're almost always at the bottom of it. The pressure exerted on your body by the weight of the atmosphere is surprisingly large. The reason you don't notice it is because the atmospheric pressure is always there. We only notice a change in pressure above or below normal atmospheric pressure (like when we fly in an airplane or go underwater in a pool). We aren't harmed by the large atmospheric pressure because our body is able to exert a force outward to balance the air pressure inward. But this means that if you were to be thrown into the vacuum of outer space by space pirates, your body pressure would continue pushing out with a large force, yet no air would be pushing in.

So would you blow up?]

You probably wouldn't blow up since your body/skin/bones are strong enough to hold you together. Still, it would be really, really uncomfortable. Besides the lack of oxygen and possible direct radiation exposure from the sun, your eyes would bulge, your eardrums could pop, and the saliva on your tongue would probably boil since the boiling point of water decreases as pressure goes down. At zero pressure your body temperature is enough to boil the water on your tongue as well as the fluid in your eyes. So basically, don't ever get caught by space pirates.

Okay, so the weight of a fluid can exert pressure on objects submerged in them, but how can we determine exactly how much pressure a fluid will exert? Consider a can of beans that got dropped in a pool as seen in the following diagram.

[Who dropped the beans?]

This is one of the great mysteries of the universe. I doubt we will ever know. If you find out, please contact the Department of Physics Mysteries immediately.

A can of beans submerged below the water to a depth h.

The weight of the column of water above the can of beans is creating pressure at the top of the can. To figure out an expression for the pressure we'll start with the definition of pressure.

$\Large P=\dfrac{F}{A}$P, equals, start fraction, F, divided by, A, end fraction

For the force $F$F we should plug in the weight of the column of water above the can of beans. The weight is always found with $W=mg$W, equals, m, g, so the weight of the column of water can be written as $W=m_{w}g$W, equals, m, start subscript, w, end subscript, g where $m_w$m, start subscript, w, end subscript is the mass of the water column above the beans. We'll plug this into the equation for pressure above and get,

$P=\dfrac{m_w g}{A}$P, equals, start fraction, m, start subscript, w, end subscript, g, divided by, A, end fraction

At this point it might not be obvious what to do, but we can simplify this expression by writing $m_w$m, start subscript, w, end subscript in terms of the density and volume of the water. Since density equals mass per volume $\rho=\dfrac{m}{V}$rho, equals, start fraction, m, divided by, V, end fraction , we can solve this for the mass of the water column and write $m_w=\rho_w V_w$m, start subscript, w, end subscript, equals, rho, start subscript, w, end subscript, V, start subscript, w, end subscript where $\rho_w$rho, start subscript, w, end subscript is the density of the water and $V_w$V, start subscript, w, end subscript is the volume of the water column above the can (not the entire volume of the pool). Plugging in $m_w=\rho_w V_w$m, start subscript, w, end subscript, equals, rho, start subscript, w, end subscript, V, start subscript, w, end subscript for the mass of the water column into the previous equation we get,

$P=\dfrac{\rho_w V_wg}{A}$P, equals, start fraction, rho, start subscript, w, end subscript, V, start subscript, w, end subscript, g, divided by, A, end fraction

At first glance this appears to have only made the formula more complex, but something magical is about to happen. We have volume in the numerator, and area in the denominator so we're going to try and cancel something here to simplify things. We know that the volume of a cylinder is $V_w=Ah$V, start subscript, w, end subscript, equals, A, h where $A$A is the area of the base of the cylinder and $h$h is the height of the cylinder. We can plug in $V_w=Ah$V, start subscript, w, end subscript, equals, A, h for the volume of water into the previous equation and cancel the areas to get,

$P=\dfrac{\rho_w (Ah)g}{A} = \rho_w h g$P, equals, start fraction, rho, start subscript, w, end subscript, left parenthesis, A, h, right parenthesis, g, divided by, A, end fraction, equals, rho, start subscript, w, end subscript, h, g

[Are we sure the areas cancel?]

Good question. The original area $A$A in the denominator was the area upon which the force is exerted, which was the area of the top of the can. The area $A$A in the numerator refers to the area of the column of water. Since the area of the column of water is equal to the area of the top of the can, these areas do in fact cancel.

Not only did we cancel the areas, we created a formula that only depends on the density of the water $\rho_w$rho, start subscript, w, end subscript, the depth below the water $h$h, and the magnitude of the acceleration due to gravity $g$g. This is really nice since nowhere does it depend on the area, volume, or mass of the can of beans. In fact, this formula doesn't depend on anything about the can of beans other than the depth it is below the surface of the fluid. So this formula would work equally well for any object in any liquid. Or, you could use it to find the pressure at a specific depth in a liquid without speaking of any object being submerged at all. You'll often see this formula with the $h$h and the $g$g swapping places like this,

${\Large P= \rho gh}$P, equals, rho, g, h

Just to be clear here, $\rho$rho is always talking about the density of the fluid causing the pressure, not the density of the object submerged in the fluid. The $h$h is talking about the depth in the fluid, so even though it will be "below" the surface of fluid we plug in a positive number. And the $g$g is the magnitude of the acceleration due to gravity which is $+9.8 \dfrac{\text{m}}{\text{s}^2}$plus, 9, point, 8, start fraction, m, divided by, s, start superscript, 2, end superscript, end fraction .

Now you might think, "OK, so the weight of the water and pressure on the top of the can of beans will push the can downward right?" That's true, but it's only a half truth. It turns out that not only does the force from water pressure push down on the top of the can, the water pressure actually causes a force that pushes inward on the can from all directions. The overall effect of the water pressure is not to force the can downward. The water pressure actually tries to crush the can from all directions as seen in the diagram below.

[Wait, but ...]

OK, if you are really clever you might have realized that the bottom of the can is slightly lower in the fluid than the top of the can, and since the pressure gets larger the deeper you go ($P_{gauge}=\rho g h$P, start subscript, g, a, u, g, e, end subscript, equals, rho, g, h) the upward pressure on the bottom of the can should be slightly larger than the downward pressure on the top of the can. This means that the overall effect of the pressure from the water is to crush the can and to exert a net upward force on it. This net upward force from the difference in pressure is the reason why there's a buoyant force on objects submerged in a fluid! But...we're getting a little ahead of ourselves so let's hold this thought for now.

A can of beans being squeezed by water pressure.

If it helps, you can think about it this way. When the can of beans fell into the water, it quite rudely displaced a large amount of water molecules from the region where the can is now. This caused the entire water level to rise. But water is pulled down by gravity which makes it want to try and find the lowest level possible. So the water tries to force itself back into the region of volume that it was displaced from in an effort to try and lower the overall height of the body of water. So, whether a can of beans (or any other object) is in the water or not, the water molecules are always being squashed into each other from the force of gravity as they try to lower the water level to the lowest point possible. The pressure $P$P in the formula $\rho gh$rho, g, h is a scalar that tells you the amount of this squashing force per unit area in a fluid.

[Hold on. Pressure is a scalar?!]

OK, so here is a subtle fact about pressure; it's defined to be a scalar, not a vector. So why do people seem to represent pressure in diagrams with arrows as if it were a vector with a particular direction?

Even though pressure is not a vector and has no direction in and of itself, the force exerted by the pressure on the surface of a particular object is a vector. So when people draw diagrams with pressure pointing in specific directions, those arrows can be thought of as representative of the direction of the forces on those surfaces exerted by the pressure from the fluid.

If there were no surface upon which the pressure could exert a force, it would make no sense to draw a direction for the force at that point inside the water. On the left hand side of the diagram below there are water molecules and pressure, but no well defined direction of force. The right hand side of the diagram below shows the well defined directions of forces on an ice cream cone submerged in the water.

While we're on the topic, we might as well make it clear that the force exerted on a surface by fluid pressure is always directed inwards and perpendicular (at a right angle) to the surface.

At this point, if you've been paying close attention you might wonder "Hey, there's air above the water right? Shouldn't the weight of the column of air above the column of water also contribute to the total pressure at the top of the can of beans?" And you would be correct. The air above the column of water is also pushing down and its weight is surprisingly large.

[How large?]

Many people think air has no mass and no weight, but that's not true. The narrow column of air with the same radius as a typical can of beans that stretches from sea level to the top of the atmosphere has a mass of around $30 \text{ kg}$30, space, k, g (that's like the weight of 30 pineapples). The force from atmospheric pressure on the top of a chessboard would be comparable to the weight of a car.

You might wonder how we can pick up the chessboard so easily if the weight of a car is pushing down on it, but it's because the weight of a car is also pushing up on it. Remember that the force from fluid pressure does not just push down, it pushes inwards perpendicular to the surface from every direction. It may not seem like there is any air under the chessboard when placed on the table but the roughness and cracks of the chess board are enough to allow air underneath. If you could get rid of all the air underneath the chessboard and prevent air from being allowed to sneak back in, that board would be stuck to the table like a suction cup. In fact, that's how suction cups work. They push the air out to create less pressure inside than out. The smooth plastic of the suction cup prevents air from sneaking back in. The higher pressure outside air pushes the suction cup into the surface. (see the diagram below)

Once air sneaks back in, the inside pressure becomes the same as the outside pressure and the cup can easily be taken off the surface.

If you wanted a formula for the total pressure (also called absolute pressure) at the top of the can of beans you would have to add the pressure from the Earth's atmosphere $P_{atm}$P, start subscript, a, t, m, end subscript to the pressure from the liquid $\rho gh$rho, g, h.

${\Large P_{total}=\rho gh +P_{atm}}$P, start subscript, t, o, t, a, l, end subscript, equals, rho, g, h, plus, P, start subscript, a, t, m, end subscript

We typically don't try to derive a fancy term like $\rho_{air} g h$rho, start subscript, a, i, r, end subscript, g, h for the atmospheric pressure $P_{atm}$P, start subscript, a, t, m, end subscript since our depth in the Earth's atmosphere is pretty much constant for any measurements made near land.

 

[Why else don't we use it?]

A problem with trying to use $\rho_{air} gh$rho, start subscript, a, i, r, end subscript, g, h to find the pressure at a certain depth in the atmosphere is that unlike the water example, the density of the air in the atmosphere is not the same at all altitudes. As you go higher in the atmosphere the density of air decreases so we can't treat $\rho_{air}$rho, start subscript, a, i, r, end subscript as a constant.

This means that the atmospheric pressure at the surface of the Earth stays relatively constant. The value of the atmospheric pressure at the surface of the Earth is stuck right around $1.01 \times10^5 Pa$1, point, 01, times, 10, start superscript, 5, end superscript, P, a. There are small fluctuations around this number caused by variations in weather patterns, humidity, altitude, etc., but for the most part when doing physics calculations we just assume that this number is a constant and stays fixed. This means, as long as the fluid you're finding the pressure for is near the surface of the Earth and exposed to the atmosphere (not in some sort of vacuum chamber) you can find the total pressure (also called absolute pressure) with this formula.

$P_{total}= \rho gh +1.01 \times 10^5 Pa$P, start subscript, t, o, t, a, l, end subscript, equals, rho, g, h, plus, 1, point, 01, times, 10, start superscript, 5, end superscript, P, a

[I don't understand this equation.]

The $\rho gh$rho, g, h corresponds to the pressure created by the weight of a liquid, and the $1.01 \times 10^5 \text{ Pa}$1, point, 01, times, 10, start superscript, 5, end superscript, space, P, a corresponds to the pressure of the Earth's atmosphere near sea level.

What's the difference between absolute pressure and gauge pressure?

When measuring pressure, people often don't want to know the total pressure (which includes atmospheric pressure). People typically want to know the difference in some pressure from atmospheric pressure. The reason is that atmospheric pressure doesn't change much and it's almost always present. So including it in your measurements can feel a bit pointless at times. In other words, knowing that the air inside of your flat tire is at an absolute pressure of

$1.01 \times 10^5 Pa$1, point, 01, times, 10, start superscript, 5, end superscript, P, a isn't really all that useful (since being at atmospheric pressure means your tire's flat). The extra pressure in the tire above atmospheric pressure is what will allow the tire to inflate and perform properly.

Because of this, most gauges and monitoring equipment use what is defined to be the gauge pressure $P_{gauge}$P, start subscript, g, a, u, g, e, end subscript . Gauge pressure is the pressure measured relative to atmospheric pressure. Gauge pressure is positive for pressures above atmospheric pressure, zero at atmospheric pressure, and negative for pressures below atmospheric pressure.

The total pressure is commonly referred to as the absolute pressure $P_{absolute}$P, start subscript, a, b, s, o, l, u, t, e, end subscript. Absolute pressure measures the pressure relative to a complete vacuum. So absolute pressure is positive for all pressures above a complete vacuum, zero for a complete vacuum, and never negative.

This can all be summed up in the relationship between the absolute pressure $P_{absolute}$P, start subscript, a, b, s, o, l, u, t, e, end subscript, gauge pressure $P_{gauge}$P, start subscript, g, a, u, g, e, end subscript, and atmospheric pressure $P_{atm}$P, start subscript, a, t, m, end subscript which looks like this,

$\Large P_{absolute} = P_{gauge} + P_{atm}$P, start subscript, a, b, s, o, l, u, t, e, end subscript, equals, P, start subscript, g, a, u, g, e, end subscript, plus, P, start subscript, a, t, m, end subscript

For the case of finding the pressure at a depth $h$h in a non-moving liquid exposed to the air near the surface of the Earth, the gauge pressure and absolute pressure can found with,

$P_{gauge}=\rho gh$P, start subscript, g, a, u, g, e, end subscript, equals, rho, g, h

$P_{absolute} = \rho g h + 1.01 \times 10^5\text{ Pa}$P, start subscript, a, b, s, o, l, u, t, e, end subscript, equals, rho, g, h, plus, 1, point, 01, times, 10, start superscript, 5, end superscript, space, P, a

Because the only difference between absolute pressure and gauge pressure is the addition of the constant value of atmospheric pressure, the percent difference between absolute and gauge pressures become less and less important as the pressures increase to very large values. (see the diagram below)

Diagram showing thevalues of various gauge and absolute pressures.

What's confusing about pressure?

People often want to plug in the density of the object submerged $\rho_{object}$rho, start subscript, o, b, j, e, c, t, end subscript into the formula for gauge pressure within a fluid $P=\rho g h$P, equals, rho, g, h, but the density in this formula is specifically referring to the density of the fluid $\rho_{fluid}$rho, start subscript, f, l, u, i, d, end subscript causing the pressure.

People often mix up absolute pressure and gauge pressure. Remember that absolute pressure is the gauge pressure plus atmospheric pressure.

Also, there are unfortunately at least 5 different commonly used units for measuring pressure (pascals, atmospheres, millimeters of mercury, etc). In physics the conventional SI unit is the pascal Pa, but pressure is also commonly measured in "atmospheres" which is abbreviated as $\text atm$a, t, m. The conversion between pascals and atmospheres is, not surprisingly, $1 \text{atm} = 1.01 \times10^5 \text{ Pa}$1, a, t, m, equals, 1, point, 01, times, 10, start superscript, 5, end superscript, space, P, a since one atmosphere is defined to be the pressure of the Earth's atmosphere.

What do solved examples involving pressure look like?

Example 1: Finding the pressure from the feet of a chair

A $7.20 \text{ kg}$7, point, 20, space, k, g fuchsia colored four legged chair sits at rest on the floor. Each leg of the chair has a circular foot with a radius of $1.30\text{cm}$1, point, 30, c, m. The well engineered design of the chair is such that the weight of the chair is equally distributed on the four feet.

Find the pressure in pascals between the feet of the chair and the floor.

$P=\dfrac{F}{A} \quad \text{(Use definition of pressure. Gauge pressure isn't applicable here since there's no fluid.)}$P, equals, start fraction, F, divided by, A, end fraction, space, left parenthesis, U, s, e, space, d, e, f, i, n, i, t, i, o, n, space, o, f, space, p, r, e, s, s, u, r, e, point, space, G, a, u, g, e, space, p, r, e, s, s, u, r, e, space, i, s, n, apostrophe, t, space, a, p, p, l, i, c, a, b, l, e, space, h, e, r, e, space, s, i, n, c, e, space, t, h, e, r, e, apostrophe, s, space, n, o, space, f, l, u, i, d, point, right parenthesis

$P=\dfrac{mg}{A} \quad \text{(Plug in formula for weight of the chair } W=mg \text{ for the force F)}$P, equals, start fraction, m, g, divided by, A, end fraction, space, left parenthesis, P, l, u, g, space, i, n, space, f, o, r, m, u, l, a, space, f, o, r, space, w, e, i, g, h, t, space, o, f, space, t, h, e, space, c, h, a, i, r, space, W, equals, m, g, space, f, o, r, space, t, h, e, space, f, o, r, c, e, space, F, right parenthesis

P=mg4×πr2(Plug in the total area of the feet of the chair 4×πr2 for the area A.)

$P=\dfrac{(7.20\text{ kg})(9.8\dfrac{\text{m}}{\text{s}^2})}{4\times \pi (0.013\text{ m})^2} \quad \text{(Plug in numbers, making sure to convert from cm to m)}$P, equals, start fraction, left parenthesis, 7, point, 20, space, k, g, right parenthesis, left parenthesis, 9, point, 8, start fraction, m, divided by, s, start superscript, 2, end superscript, end fraction, right parenthesis, divided by, 4, times, pi, left parenthesis, 0, point, 013, space, m, right parenthesis, start superscript, 2, end superscript, end fraction, space, left parenthesis, P, l, u, g, space, i, n, space, n, u, m, b, e, r, s, comma, space, m, a, k, i, n, g, space, s, u, r, e, space, t, o, space, c, o, n, v, e, r, t, space, f, r, o, m, space, c, m, space, t, o, space, m, right parenthesis

$P=\dfrac{70.56 \text{ N}}{0.002124 \text{ m}^2}=33,200 \text{ Pa} \quad \text{(Calculate, celebrate!)}$

Example 2: Force on a submarine porthole

A curious seahorse is looking into the circular window of a submarine that is sitting at a depth of $63.0 \text{ m}$63, point, 0, space, m underneath the Mediterranean sea. The density of the seawater is $1025\dfrac{\text{kg}}{m^3}$1025, start fraction, k, g, divided by, m, start superscript, 3, end superscript, end fraction. The window is circular with a radius of $5.60 \text{ cm}$5, point, 60, space, c, m. The seahorse is impressed that the window does not break from the pressure caused by the weight of the seawater.

What is the magnitude of the force exerted on the surface of the circular submarine window from the weight of the water?

$P=\dfrac{F}{A} \quad \text{(Use the definition of pressure to relate pressure to force)}$P, equals, start fraction, F, divided by, A, end fraction, space, left parenthesis, U, s, e, space, t, h, e, space, d, e, f, i, n, i, t, i, o, n, space, o, f, space, p, r, e, s, s, u, r, e, space, t, o, space, r, e, l, a, t, e, space, p, r, e, s, s, u, r, e, space, t, o, space, f, o, r, c, e, right parenthesis

$F=PA \quad \text{(Solve the formula symbolically for the force)}$F, equals, P, A, space, left parenthesis, S, o, l, v, e, space, t, h, e, space, f, o, r, m, u, l, a, space, s, y, m, b, o, l, i, c, a, l, l, y, space, f, o, r, space, t, h, e, space, f, o, r, c, e, right parenthesis

$F=(\rho gh)A \quad \text{(Plug in the formula for gauge pressure } P_{gauge}=\rho gh \text{ for the pressure P)}$F, equals, left parenthesis, rho, g, h, right parenthesis, A, space, left parenthesis, P, l, u, g, space, i, n, space, t, h, e, space, f, o, r, m, u, l, a, space, f, o, r, space, g, a, u, g, e, space, p, r, e, s, s, u, r, e, space, P, start subscript, g, a, u, g, e, end subscript, equals, rho, g, h, space, f, o, r, space, t, h, e, space, p, r, e, s, s, u, r, e, space, P, right parenthesis

$F=(1025\dfrac{\text{kg}}{m^3})(9.8\dfrac{m}{s^2})(63.0\text{ m})(\pi \times [0.056 \text{ m}]^2) \quad \text{(Plug in numbers for } \rho, g, h, \text{ and } A)$F, equals, left parenthesis, 1025, start fraction, k, g, divided by, m, start superscript, 3, end superscript, end fraction, right parenthesis, left parenthesis, 9, point, 8, start fraction, m, divided by, s, start superscript, 2, end superscript, end fraction, right parenthesis, left parenthesis, 63, point, 0, space, m, right parenthesis, left parenthesis, pi, times, open bracket, 0, point, 056, space, m, close bracket, start superscript, 2, end superscript, right parenthesis, space, left parenthesis, P, l, u, g, space, i, n, space, n, u, m, b, e, r, s, space, f, o, r, space, rho, comma, g, comma, h, comma, space, a, n, d, space, A, right parenthesis

[What?]

Since the window is circular we are going to use the formula for the area of a circle $A=\pi r^2$A, equals, pi, r, start superscript, 2, end superscript.

$F=6,230 \text{ N} \quad \text{ (Calculate, and celebrate!)}$

Note: We used the gauge pressure in this problem since the question asked for the force caused from "the weight of the water", whereas the absolute pressure would yield a force caused by the weight of the water and the weight of the air above the water.

https://www.khanacademy.org/science/physics/fluids/density-and-pressure/a/pressure-article

4.Fluid Mechanics: What is Fluid Mechanics? Mechanical Engineering

• First, What is a fluid?
• Three common states of matter are solid, liquid, and gas.
• A fluid is either a liquid or a gas.
• If surface effects are not present, flow behaves similarly in all common fluids, whether gases or liquids.
•    
• Example - The Penn State Sea Lion
  Students in the Penn State Mechanical Engineering Department have designed and built a human powered submarine, named the "Sea Lion" as part of a national contest. In the preliminary stages of the design, back in the early 1990's, some wind tunnel testing was done on various hull shapes and fin shapes. Since the submarine moves below any surface effects, it was perfectly valid to run these tests in a wind tunnel (using air as the working fluid) rather than in water (the actual fluid in which the submarine moves). As will be discussed in a later learning module, drag and lift measurements must, of course, be scaled properly according to the rules of dimensional analysis.       
• Example - PSU Harrier experiments
  Several years ago, Professor Cimbala had a research grant from NASA to study the interaction of the jet exhaust from a harrier aircraft with the ground, while the aircraft is in hover with a wind blowing. Model tests were conducted in both a wind tunnel and a water tunnel. It was perfectly valid to run these tests in either air or water, since there were no free surface effects to worry about. As will be discussed in a later learning module, the results in either case must be scaled properly according to the rules of dimensional analysis.
• Formal definition of a fluid - A fluid is a substance which deforms continuously under the application of a shear stress.
  • Definition of stress - A stress is defined as a force per unit area, acting on an infinitesimal surface element.
    • Stresses have both magnitude (force per unit area) and direction, and the direction is relative to the surface on which the stress acts.
    • There are normal stresses and tangential stresses.
    • Pressure is an example of a normal stress, and acts inward, toward the surface, and perpendicular to the surface.
    • A shear stress is an example of a tangential stress, i.e. it acts along the surface, parallel to the surface. Friction due to fluid viscosity is the primary source of shear stresses in a fluid.
    • One can construct a free body diagram of a little fluid particle to visualize both the normal and shear stresses acting on the body:
      Free Body Diagram, Fluid Particle at Rest:
      
      Consider a tiny fluid element (a very small chunk of the fluid) in a case where the fluid is at rest (or moving at constant speed in a straight line). A fluid at rest can have only normal stresses, since a fluid at rest cannot resist a shear stress. In this case, the sum of all the forces must balance the weight of the fluid element. This condition is known as hydrostatics. Here, pressure is the only normal stress which exists. Pressure always acts positively inward. Obviously, the pressure at the bottom of the fluid element must be slightly larger than that at the top, in order for the total pressure force to balance the weight of the element. Meanwhile, the pressure at the right face must be equal to that on the left face, so that the sum of forces in the horizontal direction is zero.
    • 
       [Note: This diagram is two-dimensional, but an actual fluid element is three-dimensional. Hence, the pressure on the front face must also balance that on the back face.]
      Free Body Diagram, Fluid Particle in Motion:
      
      Consider a tiny fluid element (a very small chunk of the fluid) that is moving around in some flow field. Since the fluid is in motion, it can have both normal and shear stresses, as shown by the free body diagram. The vector sum of all forces acting on the fluid element must equal the mass of the element times its acceleration (Newton's second law).
      Likewise, the net moment about the center of the body can be obtained by summing the forces due to each shear stress times its moment arm. As the size of the fluid element shrinks to "zero," i.e. negligibly small, the shear stress acting on one face of the element must be the same magnitude as those acting on the other faces. Otherwise, there would be a net moment, causing the fluid element to spin rapidly!
      [Note: To obtain force, one must multiply each stress by the surface area on which it acts, since stress is defined as force per unit area.]
  • Definition of shear stress - Shear stress is defined as a force per unit area, acting parallel to an infinitesimal surface element.
    • Shear stress is primarily caused by friction between fluid particles, due to fluid viscosity.
    • Fluids at rest cannot resist a shear stress; in other words, when a shear stress is applied to a fluid at rest, the fluid will not remain at rest, but will move because of the shear stress.
    • For a good illustration of this, consider the comparison of a fluid and a solid under application of a shear stress: A fluid can easily be distinguished from a solid by application of a shear stress, since, by definition, a fluid at rest cannot resist a shear stress.
      

      	If a shear stress is applied to the surface of a solid, the solid will deform a little, and then remain at rest (in its new distorted shape). One can say that the solid (at rest) is able to resist the shear stress.
      	Now consider a fluid (in a container). When a shear stress is applied to the surface of the fluid, the fluid will continuously deform, i.e. it will set up some kind of flow pattern inside the container. In other words, one can say that the fluid (at rest) is unable to resist the shear stress. That is to say, it cannot remain at rest under application of a shear stress.

    • Another way of saying this is: A fluid at rest cannot resist a shear stress.
    • Note, however, that a fluid at rest can resist a normal stress.
• Next, What is mechanics?
  • The dictionary says mechanics is " ... the application of the laws of force and motion ... There are two branches, statics and dynamics. ..."
• So, putting it all together, fluid mechanics is the application of the laws of force and motion to fluids, i.e. liquids and gases. There are two branches of fluid mechanics:
  • Fluid Statics or hydrostatics is the study of fluids at rest. The main equation required for this is Newton's second law for nonaccelerating bodies, i.e. .
  • Fluid Dynamics is the study of fluids in motion. The main equation required for this is Newton's second law for accelerating bodies, i.e.
  • http://www.mne.psu.edu/cimbala/Learning/Fluid/Introductory/what_is_fluid_mechanics.htm

5..The Fluid Mosaic Model

The fluid mosaic model describes the plasma membrane structure as a mosaic of phospholipids, cholesterol, proteins, and carbohydrates

Describe the fluid mosaic model of cell membranes

The main fabric of the membrane is composed of amphiphilic or dual-loving, phospholipid molecules.

Integral proteins, the second major component of plasma membranes, are integrated completely into the membrane structure with their hydrophobic membrane-spanning regions interacting with the hydrophobic region of the phospholipid bilayer.

Carbohydrates, the third major component of plasma membranes, are always found on the exterior surface of cells where they are bound either to proteins (forming glycoproteins) or to lipids (forming glycolipids).

hydrophobic

Lacking an affinity for water; unable to absorb, or be wetted by water, "water-fearing."

hydrophilic

Having an affinity for water; able to absorb, or be wetted by water, "water-loving."

amphiphilic

Having one surface consisting of hydrophilic amino acids and the opposite surface consisting of hydrophobic (or lipophilic) ones.

The fluid mosaic model was first proposed by S.J. Singer and Garth L. Nicolson in 1972 to explain the structure of the plasma membrane. The model has evolved somewhat over time, but it still best accounts for the structure and functions of the plasma membrane as we now understand them. The fluid mosaic model describes the structure of the plasma membrane as a mosaic of components —including phospholipids, cholesterol, proteins, and carbohydrates—that gives the membrane a fluid character . Plasma membranes range from 5 to 10 nm in thickness. For comparison, human red blood cells, visible via light microscopy, are approximately 8 µm wide, or approximately 1,000 times wider than a plasma membrane. The proportions of proteins, lipids, and carbohydrates in the plasma membrane vary with cell type. For example, myelin contains 18% protein and 76% lipid. The mitochondrial inner membrane contains 76% protein and 24% lipid.

The Components and functions of the Plasma Membrane

The principal components of a plasma membrane are lipids (phospholipids and cholesterol), proteins, and carbohydrates attached to some of the lipids and some of the proteins.

The fluid mosaic model of the plasma membrane

The fluid mosaic model of the plasma membrane describes the plasma membrane as a fluid combination of phospholipids, cholesterol, and proteins. Carbohydrates attached to lipids (glycolipids) and to proteins (glycoproteins) extend from the outward-facing surface of the membrane.

The main fabric of the membrane is composed of amphiphilic or dual-loving, phospholipid molecules. The hydrophilic or water-loving areas of these molecules are in contact with the aqueous fluid both inside and outside the cell. Hydrophobic, or water-hating molecules, tend to be non-polar. A phospholipid molecule consists of a three-carbon glycerol backbone with two fatty acid molecules attached to carbons 1 and 2, and a phosphate-containing group attached to the third carbon. This arrangement gives the overall molecule an area described as its head (the phosphate-containing group), which has a polar character or negative charge, and an area called the tail (the fatty acids), which has no charge . They interact with other non-polar molecules in chemical reactions, but generally do not interact with polar molecules. When placed in water , hydrophobic molecules tend to form a ball or cluster. The hydrophilic regions of the phospholipids tend to form hydrogen bonds with water and other polar molecules on both the exterior and interior of the cell. Thus, the membrane surfaces that face the interior and exterior of the cell are hydrophilic. In contrast, the middle of the cell membrane is hydrophobic and will not interact with water. Therefore, phospholipids form an excellent lipid bilayer cell membrane that separates fluid within the cell from the fluid outside of the cell.

Phospholipid aggregation

In an aqueous solution, phospholipids tend to arrange themselves with their polar heads facing outward and their hydrophobic tails facing inward.

The structure of a phospholipid molecule

This phospholipid molecule is composed of a hydrophilic head and two hydrophobic tails. The hydrophilic head group consists of a phosphate-containing group attached to a glycerol molecule. The hydrophobic tails, each containing either a saturated or an unsaturated fatty acid, are long hydrocarbon chains.

Proteins make up the second major component of plasma membranes. Integral proteins (some specialized types are called integrins) are, as their name suggests, integrated completely into the membrane structure, and their hydrophobic membrane-spanning regions interact with the hydrophobic region of the the phospholipid bilayer . Single-pass integral membrane proteins usually have a hydrophobic transmembrane segment that consists of 20–25 amino acids. Some span only part of the membrane—associating with a single layer—while others stretch from one side of the membrane to the other, and are exposed on either side. Some complex proteins are composed of up to 12 segments of a single protein, which are extensively folded and embedded in the membrane. This type of protein has a hydrophilic region or regions, and one or several mildly hydrophobic regions. This arrangement of regions of the protein tends to orient the protein alongside the phospholipids, with the hydrophobic region of the protein adjacent to the tails of the phospholipids and the hydrophilic region or regions of the protein protruding from the membrane and in contact with the cytosol or extracellular fluid.

Structure of integral membrane proteins

Integral membrane proteins may have one or more alpha-helices that span the membrane (examples 1 and 2), or they may have beta-sheets that span the membrane (example 3).

Carbohydrates are the third major component of plasma membranes. They are always found on the exterior surface of cells and are bound either to proteins (forming glycoproteins) or to lipids (forming glycolipids). These carbohydrate chains may consist of 2–60 monosaccharide units and can be either straight or branched. Along with peripheral proteins, carbohydrates form specialized sites on the cell surface that allow cells to recognize each other. This recognition function is very important to cells, as it allows the immune system to differentiate between body cells (called "self") and foreign cells or tissues (called "non-self"). Similar types of glycoproteins and glycolipids are found on the surfaces of viruses and may change frequently, preventing immune cells from recognizing and attacking them. These carbohydrates on the exterior surface of the cell—the carbohydrate components of both glycoproteins and glycolipids—are collectively referred to as the glycocalyx (meaning "sugar coating"). The glycocalyx is highly hydrophilic and attracts large amounts of water to the surface of the cell. This aids in the interaction of the cell with its watery environment and in the cell's ability to obtain substances dissolved in the water.
https://www.boundless.com/biology/textbooks/boundless-biology-textbook/structure-and-function-of-plasma-membranes-5/components-and-structure-64/fluid-mosaic-model-327-11464/







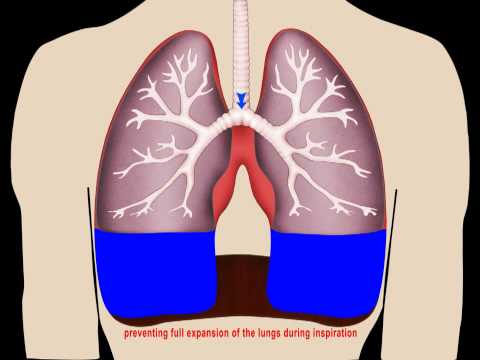
6.Fluid In Lungs

Fluid in the Chest (Pleural Effusion)

Medically Reviewed by Judith Marcin, MD on August 25, 2016 — Written by April Kahn and Ana Gotter

• Overview
• Causes
• Types
• Symptoms
• Diagnosis
• Treatment
• Treatment complications
• Cancer
• Outlook

What is pleural effusion?

Pleural effusion, also called “water on the lung,” is an excessive buildup of fluid in the space between your lungs and chest cavity. Thin membranes, called pleura, cover the outside of the lungs and the inside of the chest cavity. There’s always a small amount of liquid within this lining to help lubricate the lungs as they expand within the chest during breathing.
Certain medical conditions can cause a pleural effusion.


Pleural effusions are common, with approximately 1.5 million cases diagnosed in the United States every year, according to the American Thoracic Society. It is a serious condition associated with an increased risk of death. One study has shown that 15 percent of hospitalized people diagnosed with pleural effusions die within 30 days.

        

Causes

How does pleural effusion develop?

The pleura creates too much fluid when it’s irritated or infected. This fluid accumulates in the chest cavity outside the lung, causing what’s known as a pleural effusion.
Certain types of cancer can cause pleural effusions. Lung and breast cancer are the most common causes.
Other causes of pleural effusions include:

• congestive heart failure
• cirrhosis, or poor liver function
• pulmonary embolism, which is caused by a blood clot and is a blockage in the lung arteries
• open heart surgery complications
• pneumonia
• severe kidney disease

Types

Types of pleural effusions

There are several types of pleural effusions, with different causes and treatment options. The first classification of pleural effusions is transudative pleural effusions and exudative pleural effusions.

Transudative pleural effusions

This type is caused by fluid leaking into the pleural space as a result of either a low blood protein count or increased pressure in the blood vessels. Its most common cause is congestive heart failure.

Exudative effusions

This type is caused by:

• blocked lymph or blood vessels
• inflammation
• tumors
• lung injury

Common conditions that could result in this type of pleural infusion include pulmonary embolisms, pneumonia, and fungal infections.

Complicated and uncomplicated pleural effusions

There are also complicated and uncomplicated pleural effusions. Uncomplicated pleural effusions contain fluid without signs of infection or inflammation. They’re much less likely to cause permanent lung problems.
Complicated pleural effusions, however, contain fluid with significant infection or inflammation. They require prompt treatment that frequently includes chest drainage.

        

    

Symptoms

Symptoms and signs of pleural effusion

Some people show no symptoms of pleural effusion. These people usually find out they have the condition through chest X-rays or physical examinations ordered for another reason.
Common symptoms of pleural effusion include:

• chest pain
• dry cough
• fever
• difficulty breathing when lying down
• shortness of breath
• difficulty taking deep breaths
• persistent hiccups

See your doctor immediately if you have symptoms of pleural effusion.

Diagnosis

Diagnosing pleural effusion

Your doctor will perform a physical examination and listen to your lungs with a stethoscope. He or she may also order a chest X-ray to help diagnose pleural effusion. Other possible tests include:

• CT scan
• chest ultrasound
• pleural fluid analysis

In a pleural fluid analysis, your doctor will remove fluid from the pleural membrane area by inserting a needle into the chest cavity and suctioning the fluid into a syringe. The procedure is called a thoracentesis. The fluid will then be tested to determine the cause.
Your doctor may schedule a thoracoscopy if they discover you have a pleural effusion, but they’re unable to diagnose which type. A thoracoscopy is a surgical procedure that lets the doctor see inside the chest cavity using a fiber optic camera.
Your doctor will make a few small incisions in the chest area while you’re under general anesthesia. Then they’ll insert the camera through one incision and the surgical tool through the other incision to extract a small amount of fluid or tissue for analysis.

        

Treatment

Treating pleural effusion

The underlying cause of the condition and the severity of the effusion will determine treatment.

Draining fluid

Generally, treatment involves draining the fluid from the chest cavity, either with a needle or a small tube inserted into the chest. You’ll receive a local anesthetic before this procedure, which will make the treatment more comfortable. You may feel some pain or discomfort at the incision site after the anesthetic wears off. Most doctors will prescribe medication to help relieve pain. You may need this treatment more than once if fluid re-collects.
Other treatments may be necessary to manage fluid buildup if cancer is the cause of the pleural effusion.

Pleurodesis

Pleurodesis is a treatment that creates mild inflammation between the lung and chest cavity pleura. After drawing the excess fluid out of the chest cavity, a doctor injects a drug into the area. The drug is often talc. This medication causes the two layers of the pleura to stick together and prevents the buildup of fluid between the two layers by getting rid of the space between them.

Surgery

In more serious cases, a doctor surgically inserts a shunt, or small tube, into the chest cavity. This helps redirect the fluid from the chest to the abdomen, where it can be easily removed. Pleurectomy, in which part of the pleural lining is surgically removed, is also an option in very severe cases.

    

Treatment complications

Risks of pleural effusion treatment

Treatment for minor cases of pleural effusion is minimally invasive. Most people recover within a few days. Minor complications from treatment include slight pain and discomfort, which often go away with time. Some cases of pleural effusion can have more serious complications, depending on the severity of the condition and treatment used.
Serious complications include:

• pulmonary edema or fluid in the lungs, which can result from draining fluid too quickly during thoracentesis
• partial collapsed lung
• infection or bleeding

These complications, while serious, are very rare. Your doctor will help determine the most effective treatment option and will discuss the benefits and risks of each procedure.

    

Pleural effusions and cancer

Pleural effusions can be the result of cancer cells spreading to the pleura. They can also be the result of cancer cells blocking the flow of normal fluid within the pleura. Fluid may also build up as a result of certain cancer treatments, such as radiation therapy or chemotherapy.
Certain cancers are more likely to cause pleural effusions than others, including:

• lung cancer
• breast cancer
• ovarian cancer
• leukemia
• melanoma
• cervical cancer
• uterine cancer

Signs and symptoms include:

• shortness of breath
• cough
• chest pain

Pleurodesis is often used as a treatment for the malignant pleural effusions caused by cancer. Antibiotics may also be used if you have or are susceptible to an infection. Steroids or other anti-inflammatory medications may be used to reduce pain and inflammation.
In addition to treating the pleural effusion, your doctor will treat the cancer that caused it. Pleural effusions are typically the result of metastatic cancer.
People who are undergoing treatment for cancer may also have compromised immune systems, making them more prone to infections or other complications.

Outlook

What is the outlook for a pleural effusion?

Pleural effusions can be serious and life-threatening. Many require hospitalized treatment and some require surgery. The time it takes to recover from pleural effusions depends on the cause, size, and severity of the effusion, as well as your overall health.


You will begin your recovery in the hospital, where you’ll receive the necessary medication and care to help you begin to recover. Many people report feeling tired and weak in the first week after they’ve been discharged from the hospital. On average, you will see your incision sites from surgery heal within two to four weeks.